实证方法:倾向值匹配+双重差分(PSM-DID)
本教程为简明PSM-DID教程,适合初学者。本文首先简述PSM和DID的原理,最后讲如何实际操作,附有stata代码。
一、为什么要进行倾向值匹配?
倾向值匹配后的分析可以进一步确定两者之间的因果性。
反事实理论框架(counterfactual framework)
反事实理论框架是指同一个体既在实验组又在控制组。举一个简单的例子,假如我们探讨是否上过大学对薪资的影响。不考虑现实因素,我们最佳的做法是先统计一批上过大学的人的薪资,再统计同一批人没有上过大学的薪资。但是一个人不可能既上过大学又没上过大学,所以这个研究框架是反事实的,也就是反事实理论框架。如果我们在研究中能够找到除了核心自变量(是否上过大学)以外,其他特征(性别、年龄、籍贯、家庭年收入等)都相似的两个个体A和B。我们就可以把A和B的薪资当做同一个个体上过大学的薪资和没上过大学的薪资,由于AB二者除了是否上过大学以外其他特征均相似,所以我们可以认为最终分析结果可以确定是否上过大学与薪资之间不仅仅是简单的相关关系,还具有因果关系。而倾向值匹配方法PSM则是一种帮助我们根据上过大学的A的特征(实验组),找到与之对应没上过大学的B(控制组)的方法。
二、倾向值匹配的步骤
(一)选择协变量
什么是协变量呢?联系上文例子,协变量就是用来匹配A和B的特征,如性别、年龄、籍贯等等,在我们(经管小硕)的论文里,一般选择做回归时的控制变量就行了。
(二)估计倾向值
倾向值匹配方法就是根据倾向值的近似程度来进行匹配,所以在匹配前需要计算倾向值。倾向值是通过协变量回归得到的,我们常用的回归模型有Logit回归模型和Probit回归模型,此处给出上述例子的Logit模型如下图所示,其中X表示协变量矩阵。

通过估计,我们可以得到协变量各个系数的具体取值,从而得到各个样本的倾向值得分(stata可以计算,具体计算原理不必知道)。
(三)根据倾向值进行匹配
这一步骤有很多匹配方法,包括邻近匹配、半径匹配、核心匹配、分层匹配等等。我们比较常用的就是邻近匹配,即通过实验组A的倾向值a,从对照组中找到与a最相近的倾向值b所对应的个体B。
三、PSM-DID
(一)双重差分
双重差分是指组内差分和组间差分。扩展一下上述例子,我们研究1996年至2006年城市居民是否上过大学对薪资的影响,其中在1999年颁布了大学扩招政策。在这个例子中,组间差分指的是同一时期内实验组个体A和控制组个体B之间的差异;组内差分指的是实验组或控制组个体在1999年扩招政策实施前后的差异。DID模型的一般形式如下,其中treated为标记个体是否为实验组的虚拟变量,time是标记政策是否实施的虚拟变量,did为两者的交互向:
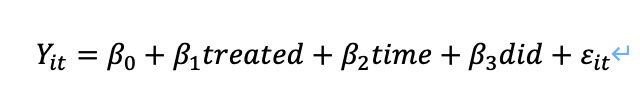
(二)倾向值匹配双重差分
通过上述原理的讲解,我们可以大致了解到双重差分法是针对面板数据的,而倾向值匹配法则适用于截面数据。为了解决这一问题,现有文献主要有两种主流的解决办法。
- 方法一:将面板视为截面数据,直接进行匹配。
- 方法二:将面板数据逐年拆分成截面数据,进行逐年匹配,之后再合并成面板数据。
这两种做法都有利有弊,实际使用中可以看哪个结果好就使用哪个。
四、PSM-DID的Stata实现
1.如果是第一次使用psmatch2命令,需要在stata中输入以下代码进行安装。
1 | |
2.之后进行倾向值匹配,代码如下。获得的结果可以根据相关论文进行取舍。
1 | |
3.进行psmatch2之后我们可以得到三部分结果。分别为:
- 第一部分:logit回归结果。
- 第二部分:ATT,ATU和ATE的值。我们主要关注ATT的t-stat,只要t的绝对值大于1.64即可说明匹配结果显著。
- 第三部分:报告两组在共同取值范围内的样本量。一般论文不展示此结果。
4.进行平衡性检验。
1 | |
此处结果主要参考匹配前后的%bias是否大幅下降,以及%reduct|bia|的大小(一般来说越接近100%表示匹配质量越好)
5.双重差分
1 | |